Idee: Geduld ist eine unscheinbare Form von Reichtum.
[Rente]
Aufzinsungstabelle. Wirkung von Zinseszins: Was wird aus 1.000 Euro nach 5, 10, 20 oder 30 Jahren?
Die Aufzinstabelle (unten im Text) stelle ich hier als JPG-Datei gemeinfrei zur Verfügung ©2026, Thomas Jacob
Die Aufzinstabelle als gesellschaftliches Gedankenexperiment
➡️ Die heutige Präsentation einer sogenannten Aufzinstabelle, welche den realistischen Effekt des Zinseszinses sichtbar macht, möchte ich einmal in eine größere Diskussion stellen: in jene um die langfristige Organisation unserer Altersvorsorge.
Nicht polemisch.
Nicht programmatisch.
Sondern nüchtern – als Gedankenexperiment.
Eine einfache Ausgangsannahme
Nehmen wir an, eine vernunftgesteuerte Gesellschaft würde jedem neugeborenen Mitbürger zu seinem ersten Geburtstag eine Geldsumme schenken.
Sagen wir: den Betrag eines durchschnittlichen Monatsverdienstes.
Diese Summe würde weder konsumiert noch politisch umverteilt, sondern langfristig angelegt – etwa in einem weltweit diversifizierten Aktienfonds.
Die Verwaltung erfolgte treuhänderisch, in Form einer öffentlichen unabhängigen Treuhandstiftung, rechtlich klar gebunden, außerhalb unmittelbarer staatlicher Verfügung und zugleich professionell geführt.
Historische Durchschnittswerte sprechen bei breit gestreuten Aktienanlagen häufig von rund acht Prozent jährlicher Wertentwicklung – Dividenden noch nicht einmal eingerechnet.
Was geschieht also, wenn eine solche Anfangssumme sechzig Jahre unangetastet bleibt?
Der lange Horizont
Die Antwort liefert keine Ideologie – sondern eine Aufzinstabelle.
Sie zeigt nüchtern, wie aus einem einmaligen Betrag über sechs Jahrzehnte ein Vermögen entstehen kann, das als eine Art „Rentenbonus“ dienen könnte: nicht als Vollversorgung, sondern als stabile Ergänzung.
Sechzig Jahre sind im politischen Betrieb eine Ewigkeit – für vermögensverwaltende Treuhandstiftungen das Tagesgeschäft.
Für ein Neugeborenes sind sie schlicht Lebenszeit.
Und genau hierin liegt der stille Reiz der Aufzinstabelle:
Sie zwingt die Betrachtung in den langen Horizont und in andere Denkstrukturen.
Der zweite Blick: Kaufkraft
Zur Ehrlichkeit gehört die Gegenrechnung.
Inflation ist kein Gerücht.
Nehmen wir hypothetisch drei Prozent Kaufkraftverlust pro Jahr an. Auch diese Entwicklung lässt sich in derselben Tabelle abbilden.
Wir rechnen also nicht nur die nominale Verzinsung hoch –
wir rechnen ebenso den Kaufkraftverlust gegen.
Was übrig bleibt, ist keine Fantasie.
Sondern Mathematik.
Verwaltungskosten – heute und morgen
Ein Einwand betrifft regelmäßig die Verwaltungskosten.
Doch auch hier lohnt ein ruhiger Blick:
Bereits heute lassen sich breit gestreute Fonds zu vergleichsweise geringen Kosten führen. Mit dem weiteren Einsatz automatisierter Prozesse und künstlicher Intelligenz dürfte die Verwaltung komplexer Portfolios künftig auf ein Niveau sinken, das aus heutiger Sicht kaum vorstellbar erscheint.
Eine offene Frage
Und vielleicht ist genau das der eigentliche Zweck dieser Aufzinstabelle.
Nicht, um fertige Antworten zu liefern.
Nicht, um politische Programme zu skizzieren.
Sondern um eine einfache Frage in den Raum zu stellen:
Was würde geschehen, wenn man einem Neugeborenen einmalig einen Betrag in Höhe eines durchschnittlichen Monatsverdienstes mit auf den Weg gäbe – langfristig angelegt, über sechzig Jahre nicht angerührt?
Acht Prozent durchschnittliche Wertsteigerung werden häufig genannt.
Drei Prozent Kaufkraftverlust ebenso.
Die Zahlen stehen in der Tabelle.
Man kann sie nachschlagen.
Man kann sie selbst durchrechnen.
Man kann sie weiterdenken.
Mehr nicht.
Denn manchmal genügt es, eine Rechenhilfe bereitzustellen –
und dem Leser zuzutrauen, dass er den Gedanken selbst zu Ende führt.
Was wird aus 1.000 EUR, wenn sie n Jahre lang jährlich mit Zinseszins wachsen?
Formel: 1.000 EUR × (1 + i)ⁿ · i = Zinssatz pro Jahr (z. B. 0,05 = 5 %) · n = Jahre. Werte auf drei Nachkommastellen gerundet – ohne Steuern, Gebühren und Inflation.
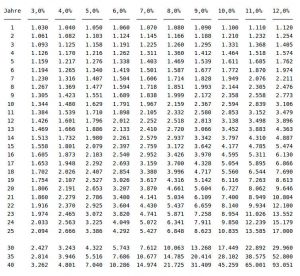
Aufzinsungstabelle – Endwert von 1 EUR nach n Jahren bei jährlichem Zinseszins
Formel: Endwert = 1 × (1 + i)n – i = jährlicher Zinssatz
| Jahre | 3,0 % | 4,0 % | 5,0 % | 6,0 % | 7,0 % | 8,0 % | 9,0 % | 10,0 % | 11,0 % | 12,0 % |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1,030 | 1,040 | 1,050 | 1,060 | 1,070 | 1,080 | 1,090 | 1,100 | 1,110 | 1,120 |
| 2 | 1,061 | 1,082 | 1,103 | 1,124 | 1,145 | 1,166 | 1,188 | 1,210 | 1,232 | 1,254 |
| 3 | 1,093 | 1,125 | 1,158 | 1,191 | 1,225 | 1,260 | 1,295 | 1,331 | 1,368 | 1,405 |
| 4 | 1,126 | 1,170 | 1,216 | 1,262 | 1,311 | 1,360 | 1,412 | 1,464 | 1,518 | 1,574 |
| 5 | 1,159 | 1,217 | 1,276 | 1,338 | 1,403 | 1,469 | 1,539 | 1,611 | 1,685 | 1,762 |
| 6 | 1,194 | 1,265 | 1,340 | 1,419 | 1,501 | 1,587 | 1,677 | 1,772 | 1,870 | 1,974 |
| 7 | 1,230 | 1,316 | 1,407 | 1,504 | 1,606 | 1,714 | 1,828 | 1,949 | 2,076 | 2,211 |
| 8 | 1,267 | 1,369 | 1,477 | 1,594 | 1,718 | 1,851 | 1,993 | 2,144 | 2,305 | 2,476 |
| 9 | 1,305 | 1,423 | 1,551 | 1,689 | 1,838 | 1,999 | 2,172 | 2,358 | 2,558 | 2,773 |
| 10 | 1,344 | 1,480 | 1,629 | 1,791 | 1,967 | 2,159 | 2,367 | 2,594 | 2,839 | 3,106 |
| 15 | 1,558 | 1,801 | 2,079 | 2,397 | 2,759 | 3,172 | 3,642 | 4,177 | 4,785 | 5,474 |
| 20 | 1,806 | 2,191 | 2,653 | 3,207 | 3,870 | 4,661 | 5,604 | 6,727 | 8,062 | 9,646 |
| 25 | 2,094 | 2,666 | 3,386 | 4,292 | 5,427 | 6,848 | 8,623 | 10,835 | 13,585 | 17,000 |
| 30 | 2,427 | 3,243 | 4,322 | 5,743 | 7,612 | 10,063 | 13,268 | 17,449 | 22,892 | 29,960 |
| 35 | 2,814 | 3,946 | 5,516 | 7,686 | 10,677 | 14,785 | 20,414 | 28,102 | 38,575 | 52,800 |
| 40 | 3,262 | 4,801 | 7,040 | 10,286 | 14,974 | 21,725 | 31,409 | 45,259 | 65,001 | 93,051 |
| 50 | 4,384 | 7,107 | 11,467 | 18,420 | 29,457 | 46,902 | 74,358 | 117,391 | 184,565 | 289,002 |
| 60 | 5,892 | 10,520 | 18,679 | 32,988 | 57,946 | 101,257 | 176,031 | 304,482 | 524,057 | 897,597 |
i = jährlicher Zinssatz (z. B. 0,05 bei 5 %), n = Anzahl der Jahre
Bei sehr langen Laufzeiten (50–60 Jahre) wird der Zinseszinseffekt besonders deutlich – besonders bei höheren Zinssätzen.
Die 72er-Regel
Keine Aufzinsungstabelle zur Hand? Kein Problem! Es gibt eine verblüffend einfache Faustformel, mit der du im Kopf ausrechnen kannst, wie lange es dauert, bis sich dein Geld verdoppelt.
So funktioniert die Formel:
Teile einfach die Zahl 72 durch den Zinssatz, den du erwartest. Das Ergebnis ist die ungefähre Anzahl an Jahren, die dein Kapital zur Verdopplung benötigt.
Jahre bis zur Verdopplung ≈ 72 : Zinssatz
Ein paar Beispiele aus der Praxis. Verdopplung in Jahren:
- Bei 2 % Zinsen: 72 : 2 = 36 Jahre
- Bei 4 % Zinsen: 72 : 4 = 18 Jahre
- Bei 6 % Zinsen: 72 : 6 = 12 Jahre
- Bei 8 % Zinsen: 72 : 8 = 9 Jahre
Warum das hilfreich ist: Die Regel macht den Zinseszins-Effekt greifbar. Sie zeigt sofort, dass schon eine kleine Steigerung des Zinssatzes (z. B. von 2 % auf 4 %) die Zeit bis zur Verdopplung deines Vermögens nicht nur ein bisschen verkürzt, sondern direkt halbiert.
Die äquivalente Aufzinsungstabelle – jetzt aber mit monatlichem Zinseszins
(also monatliche Verzinsung und sofortige Reinvestition zur Denkmodell-Erweiterung)
Das entspricht der Idee: Jeden Monat wird der Zins (z. B. 12 % p.a. → 1 % pro Monat) gutgeschrieben und sofort wieder mitverzinst.
Monatliche Verzinsung und sofortige Reinvestition – z. B. 12 % p.a. nominal → 1 % pro Monat
| Jahre | 3,0 % | 4,0 % | 5,0 % | 6,0 % | 7,0 % | 8,0 % | 9,0 % | 10,0 % | 11,0 % | 12,0 % |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1,030 | 1,041 | 1,051 | 1,062 | 1,072 | 1,083 | 1,094 | 1,105 | 1,116 | 1,127 |
| 2 | 1,062 | 1,083 | 1,105 | 1,127 | 1,150 | 1,173 | 1,196 | 1,220 | 1,245 | 1,270 |
| 3 | 1,094 | 1,127 | 1,161 | 1,197 | 1,233 | 1,270 | 1,309 | 1,348 | 1,389 | 1,431 |
| 4 | 1,127 | 1,173 | 1,221 | 1,270 | 1,322 | 1,376 | 1,431 | 1,489 | 1,550 | 1,612 |
| 5 | 1,162 | 1,221 | 1,283 | 1,349 | 1,418 | 1,490 | 1,566 | 1,645 | 1,729 | 1,817 |
| 10 | 1,349 | 1,491 | 1,647 | 1,819 | 2,010 | 2,220 | 2,451 | 2,707 | 2,989 | 3,300 |
| 15 | 1,567 | 1,820 | 2,114 | 2,454 | 2,849 | 3,307 | 3,838 | 4,454 | 5,168 | 5,996 |
| 20 | 1,821 | 2,223 | 2,713 | 3,310 | 4,039 | 4,927 | 6,009 | 7,328 | 8,935 | 10,893 |
| 25 | 2,115 | 2,714 | 3,481 | 4,465 | 5,725 | 7,340 | 9,408 | 12,057 | 15,448 | 19,788 |
| 30 | 2,457 | 3,313 | 4,468 | 6,023 | 8,116 | 10,936 | 14,731 | 19,837 | 26,708 | 35,950 |
| 35 | 2,854 | 4,046 | 5,734 | 8,124 | 11,506 | 16,293 | 23,063 | 32,639 | 46,176 | 65,310 |
| 40 | 3,315 | 4,940 | 7,358 | 10,957 | 16,311 | 24,273 | 36,110 | 53,701 | 79,834 | 118,648 |
| 50 | 4,468 | 7,389 | 12,182 | 20,085 | 33,003 | 54,034 | 88,668 | 144,889 | 236,736 | 386,968 |
| 60 | 6,022 | 10,936 | 19,837 | 35,950 | 64,896 | 116,985 | 210,034 | 376,138 | 672,749 | 1.200.000 |
Zum Vergleich – effektiver Jahreszins bei monatlicher Verzinsung
(statt nominaler 12 % p.a. → real ~12,68 % effektiv)
Bei sehr langen Laufzeiten (50–60 Jahre) wird der Unterschied zum jährlichen Zinseszins besonders groß – bei 12 % nominal wächst 1 € in 60 Jahren monatlich verzinst auf über 1,2 Millionen EUR.
—
Thomas Jacob · Erstveröffentlichung: 11.2.2026
▶️ Lies auch: „Das Inhortas-Rentenmodell – Zeitgemäße Altersvorsorge mit Grundrente und Vorsorgekonto“ (28.5.2025)